Geometric Decomposition Coil Compression
This is a demo of the ESPIRiT Coil Compression (ECC). It is based on the abstract: D. Bahri et. al, "ESPIRiT-Based Coil Compression for Cartesian Sampling" ISMRM 2013 pp:2657
The demo shows how to use the compression and in addition it shows the use of alignment of the compression matrices. The example is on 2D data, but can also be applied on 3D as well. ECC removes correlations between channels along a fully sampled readout dimension. This allows for significant reduction in data, so parallel imaging and other multi-channel algorithms are much more computationally efficient. This demo demonstrate effective compression from 32->5 virtual channels. ECC has better noise properties than GCC.
Contents
Set parameters:
load brain_32ch.mat % number of compressed virtual coils ncc = 5; dim = 2; ncalib = 24; % use 24 calibration lines to compute compression [sx,sy,Nc] = size(DATA); slwin = 4; % sliding window length for GCC dispm = [4,8]; % diplay matrix settings % crop calibration data calib = crop(DATA,[ncalib,sy,Nc]);
ECC - ESPIRiT Coil Compression (with no alignment)
This code computes ECC compression matrices from calibration data. The data is the transformed to the new compressed virtual coils basis.
eccmtx = calcECCMtx(calib,dim,ncc); % compress the data ECCDATA = CC(DATA,eccmtx,dim); % compute coil image ECCim = ifft2c(ECCDATA); % Also compute GCC for comparison gccmtx = calcGCCMtx(calib,dim,slwin); % compress the data GCCDATA = CC(DATA,gccmtx,dim); % compute coil image GCCim = ifft2c(GCCDATA);
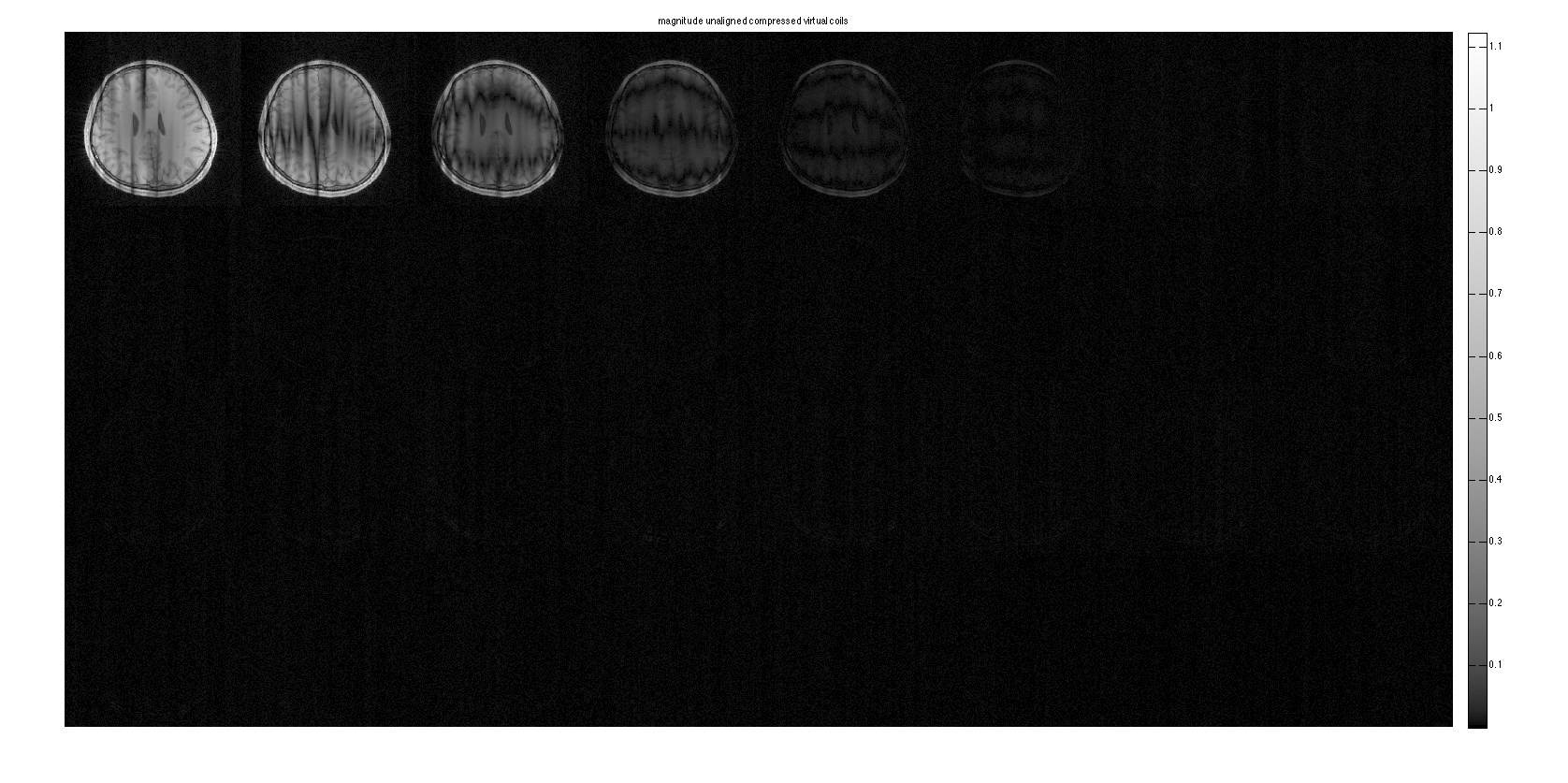
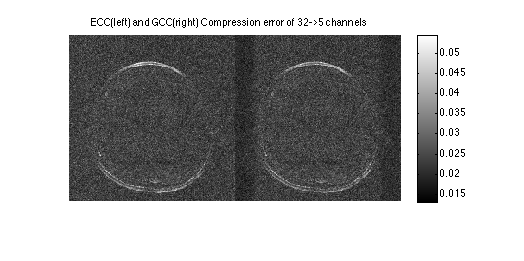
The compressed virtual coil domain shows that the data can be represented effectively by 5 out of 32 channels. The error is much lower than in SCC.
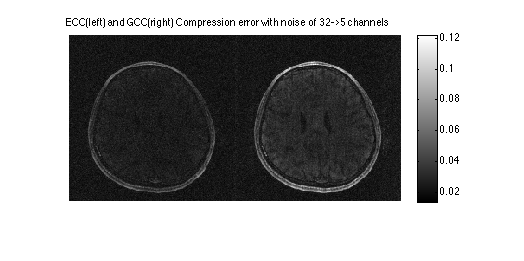
Note that the ECC error image is noisier than the GCC. This is because more noise is left out of image, whereas GCC is biased and fits some noise.
Note that the colormap is non-linear to improve dynamic-range of the visualization.
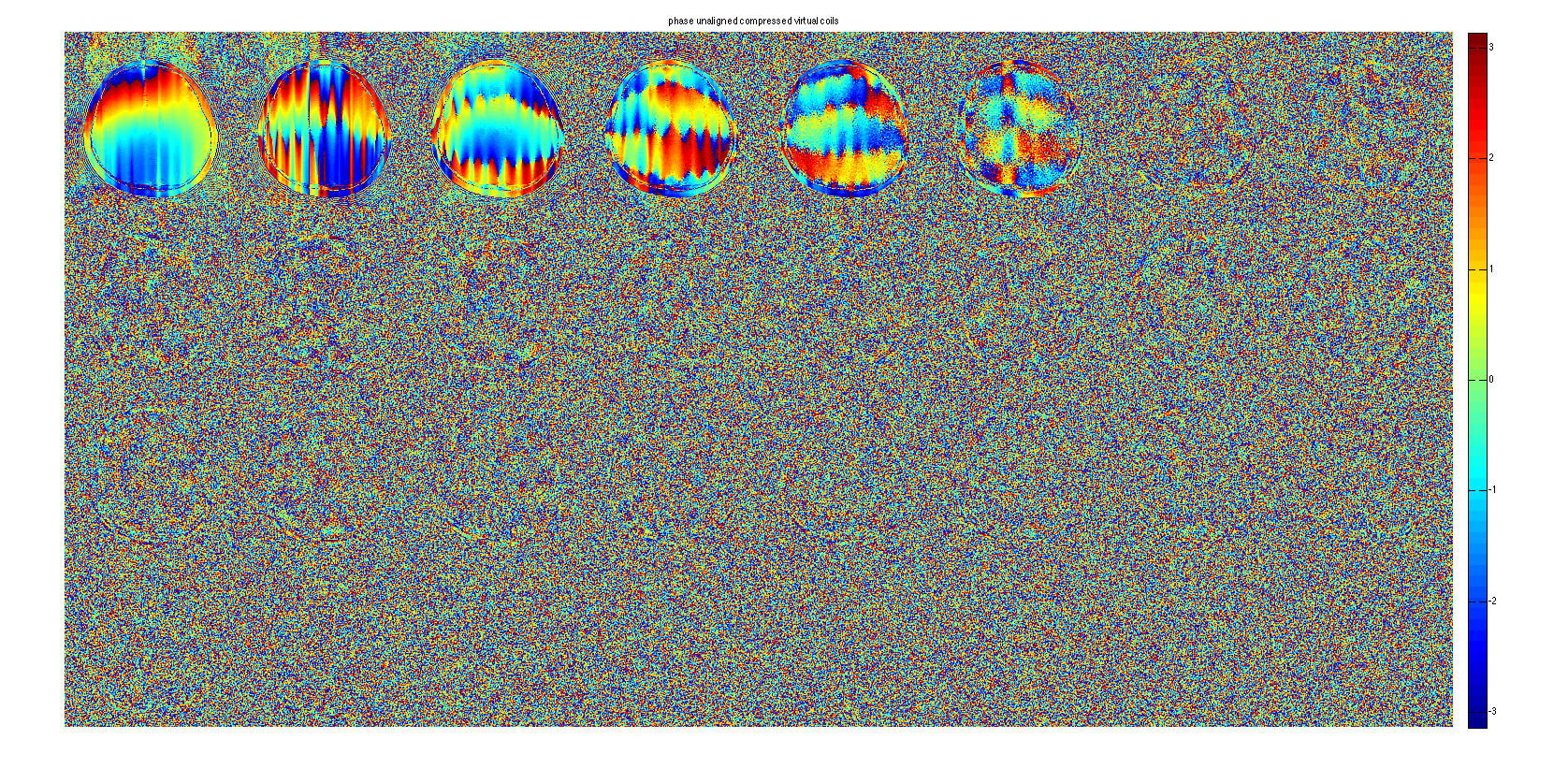
figure, imshow3(abs(ECCim),[],dispm); title('magnitude unaligned compressed virtual coils'); colormap(sqrt(gray(256))); colorbar; figure, imshow3(angle(ECCim),[],dispm); title('phase unaligned compressed virtual coils'); colormap('default'); colorbar figure, imshow(cat(2,sos(ECCim(:,:,ncc+1:end)),sos(GCCim(:,:,ncc+1:end))),[]); colorbar; title('ECC(left) and GCC(right) Compression error of 32->5 channels')
ESPIRiT Coil Compression (with alignment)
Here, we crop the compression matrices so they compress from 32->5 channels. We then align the matrices so they smoothly vary. This does not change the subpspace of the data -- only rotates the basis vectors.
Note that the colormap is non-linear to improve dynamic-range of the visualization.
% crop and align matrices eccmtx_aligned = alignCCMtx(eccmtx(:,1:ncc,:)); % compress the data ECCDATA_aligned = CC(DATA,eccmtx_aligned, dim); % compute coil image ECCim_aligned = ifft2c(ECCDATA_aligned);
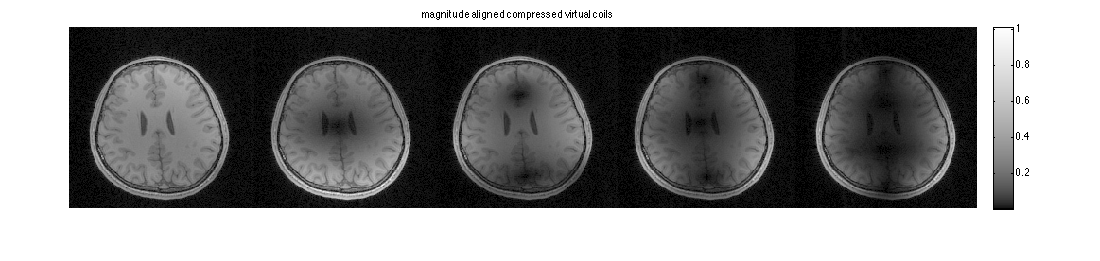
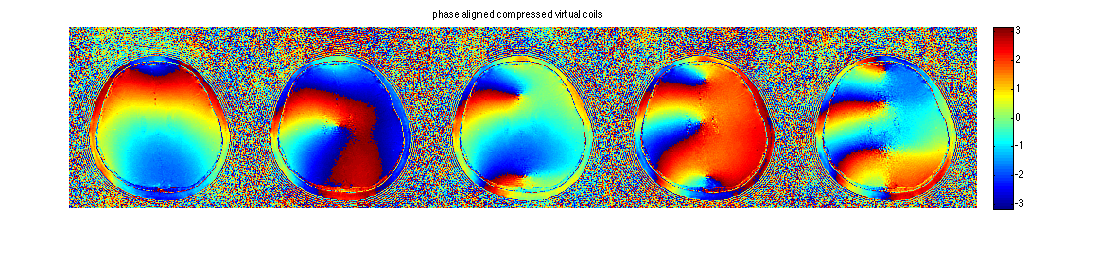
The compressed virtual coil are now smooth in phase and magnitude
figure, imshow3(abs(ECCim_aligned),[],[1,ncc]); title('magnitude aligned compressed virtual coils'); colormap(sqrt(gray(256))); colorbar; figure, imshow3(angle(ECCim_aligned),[],[1,ncc]); title('phase aligned compressed virtual coils'); colormap('default'); colorbar
ECC - ESPIRiT Coil Compression with added noise
Here we add noise to the calibration data -- compute ECC and GCC compression matrices and then use them to compress the original data.
ECCerr = zeros(15,1); GCCerr = zeros(15,1); sigma = logspace(log10(0.001),log10(0.05),15); % repear compression for increased noise levels and comput squared error for n=1:15 calib_n = calib + randn(size(calib))*sigma(n)/sqrt(2) + 1i*randn(size(calib))*sigma(n)/sqrt(2); eccmtx = calcECCMtx(calib_n,dim,ncc,6); % compress the data ECCDATA = CC(DATA,eccmtx,dim); % compute coil image ECCim = ifft2c(ECCDATA); % Also compute GCC for comparison gccmtx = calcGCCMtx(calib_n,dim,slwin); % compress the data GCCDATA = CC(DATA,gccmtx,dim); % compute coil image GCCim = ifft2c(GCCDATA); ECCerr(n) = sum(sum(sos(ECCim(:,:,ncc+1:end)).^2)); GCCerr(n) = sum(sum(sos(GCCim(:,:,ncc+1:end)).^2)); end
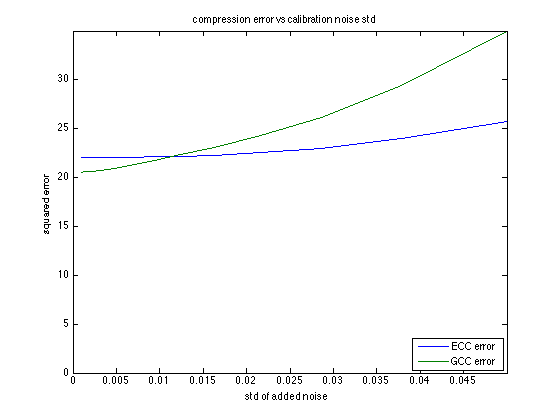
GCC has slightly lower error for low level of noise. However, ECC has quite stable performance with increasing noise, whereas GCC is degrading rapidly.
figure, plot(sigma,ECCerr,sigma,GCCerr) title('compression error vs calibration noise std') xlabel('std of added noise') ylabel('squared error'); axis([0,sigma(end),0,max(GCCerr(end),ECCerr(end))]) legend('ECC error', 'GCC error','Location','SouthEast'); figure, imshow(cat(2,sos(ECCim(:,:,ncc+1:end)),sos(GCCim(:,:,ncc+1:end))),[]); colorbar; title('ECC(left) and GCC(right) Compression error with noise of 32->5 channels')